
Have you ever wondered why the direction of sunset changes throughout the year? We usually speak of the sun setting in the west, but technically it only sets due west at the spring and autumn equinoxes. For the rest of the year, the direction of sunset pivots about this westerly point, moving northerly in winter, and towards the south in summer. (In the northern hemisphere, the sunset tends more northerly in summer and more southerly in winter.)
Technically the sun only sets due west at the spring and autumn equinoxes.
If you’re an early riser, you’ll have noticed that the same symmetries apply to the easterly directions of sunrise. But it must have taken years for ancient astronomers to notice the particulars of all these patterns, let alone explain them astronomically.

One of the earliest records of such an observation may lie in the alignment of the Wurdi Youang stone circle in Victoria, on land traditionally owned by the Wathaurong people. The circle’s age is unknown, but it could be as old as 11,000 years, and researchers – including former Monash academic Duane Hamacher – think it's likely that the circle includes deliberate markers of the direction of sunset at the solstices and equinoxes.
We’ll never know just why, or even if, the builders of Wurdi Youang, Stonehenge, and other stone arrangements marked out the directions of sunrise or sunset at solstices and equinoxes. But historians do know that ancient Greek-speaking people deduced an extraordinary amount of astronomical information from the way the sunset and sunrise directions change throughout the year.
Most of the early Greek astronomical manuscripts have been lost, but their content was developed and codified by Claudius Ptolemy, about 150CE, in a book known as Almagest. It’s one of those ancient Greek classics that owe their survival to mediaeval Arabic scholars. Its first printed appearance, in Venice in 1515, was based on a mediaeval Latin translation of the Arabic adaptation of the original Greek – quite a multicultural achievement!
Read more: The circadian rhythm of life: ‘If we disrupt the light cycle, then you’ll die earlier’
Among many other things Ptolemy was interested in was the fact that the symmetry in the arc of sunset directions is reflected in the symmetry between the sun’s midday altitude at the summer and winter solstices. The sunset direction reaches its northerly and southerly extremes at the solstices, while the noon altitudes are also at their extremes (highest and lowest) at the solstices. The midpoints in both cases occur at the equinoxes.
Thanks largely to Hipparchus of Nicaea – who worked about 150BCE, and to whom Ptolemy was indebted – astronomers had already figured out the geometrical configuration of the equinoxes. To do this, they used the concept of two imaginary planes cutting through a huge imaginary “celestial sphere” centred on the Earth. You can get the idea by visualising a third, more obvious plane – an extension of the one we appear to be standing on, bounded by the horizon with the sky sitting on top like a hemispherical dome.
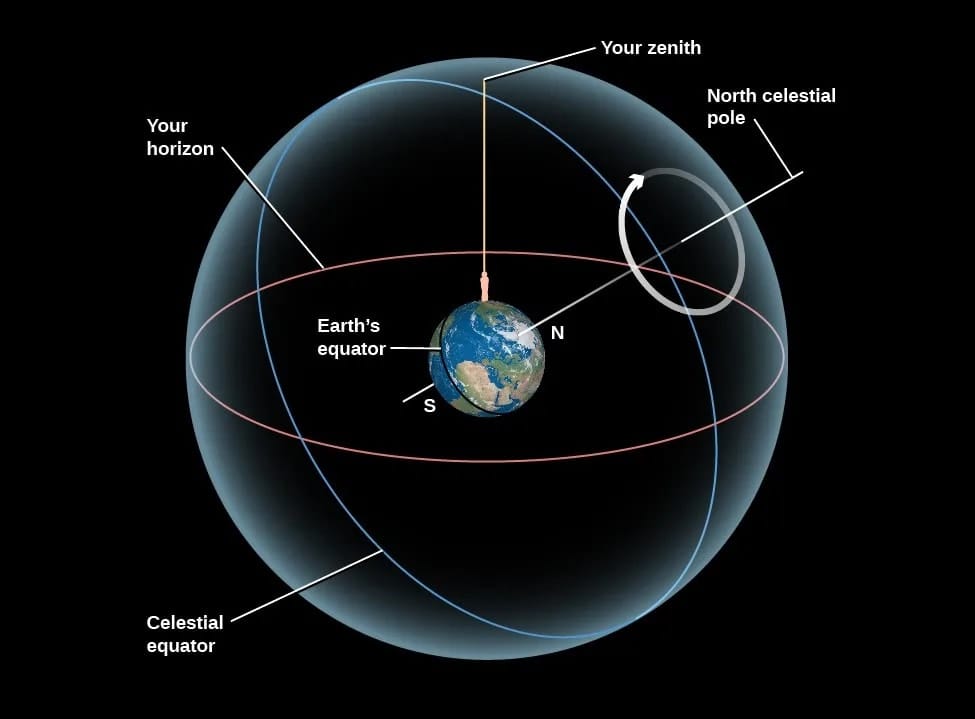
The first plane is that of the “celestial equator”, which is parallel to the plane of the Earth’s equator. This is the plane in which the sun appears to make its daily journey about Earth, from sunrise to sunset and on through the night until sunrise again.
Today, following pioneers such as Nicolas Copernicus, we can imagine this more easily, because we know it’s not the sun that is moving but the Earth, which is rotating on its axis from west to east – that is, in the plane of the equator – producing the illusion that the sun rises and sets each day.
Read more: Leap years, equinoxes and dates: A very short history of the calendar
The second plane is that of the “ecliptic”, the sun’s apparent yearly path around the Earth. It must have seemed strange to the ancients that the sun had two different paths in its journey about the Earth. Still, these astronomers had figured out that these two paths lay in two different, intersecting planes. The equinoxes and the directions of sunset show why.
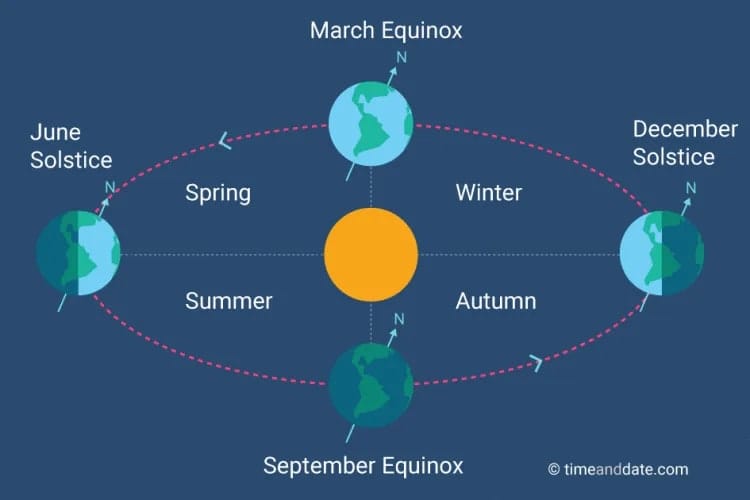
The equinoxes occur when the sun sets due west, and the days and nights are (virtually) of equal length everywhere on Earth. At the equator, however, the days and nights are always 12 hours long, so the spring and autumn equinoxes must happen when the sun is “on” the equator. So, in its yearly journey along the ecliptic, there are only two days when the sun crosses the equator. Which means that the ecliptic and equator must be in different planes, and must intersect at the equinoxes.
The equinoxes occur when the sun sets due west, and the days and nights are (virtually) of equal length everywhere on Earth.
Ptolemy’s goal was to calculate the angle between these two imaginary planes, so that the celestial equator and ecliptic could be represented accurately – via an armillary sphere, for example. Like the Babylonians and others before them, the Greeks wanted to be able to keep track of the stars and planets, in order to study the ways of the deities who ruled them, and also to help with navigation.
Ptolemy reasoned as follows. At the equinoxes – when the direction of the sunset is halfway between the most northerly and southerly sunset points – the sun is at the point of intersection of the ecliptic and the celestial equator, as I mentioned. So the angle between these two intersecting planes must be half the difference between the summer and winter solstice solar altitudes, which exhibit the same symmetry.
He measured this angle to be about 23°40', or 23.67°, in the ballpark of a value found earlier by Aristarchus of Samos (whose maverick heliocentric theory of planetary motion had inspired Copernicus).
It was an incredible deduction, even if Ptolemy did believe that the planets and stars, including the sun, literally moved around the Earth. Today, of course, we believe it's the Earth that's moving in the plane of the ecliptic, not the sun. Astronomers also have a more up-to-date figure for the angle of tilt, 23.44°. (The change since Ptolemy’s time is largely because of the phenomenon of “precession”, a slow rotation of the Earth’s axis.)
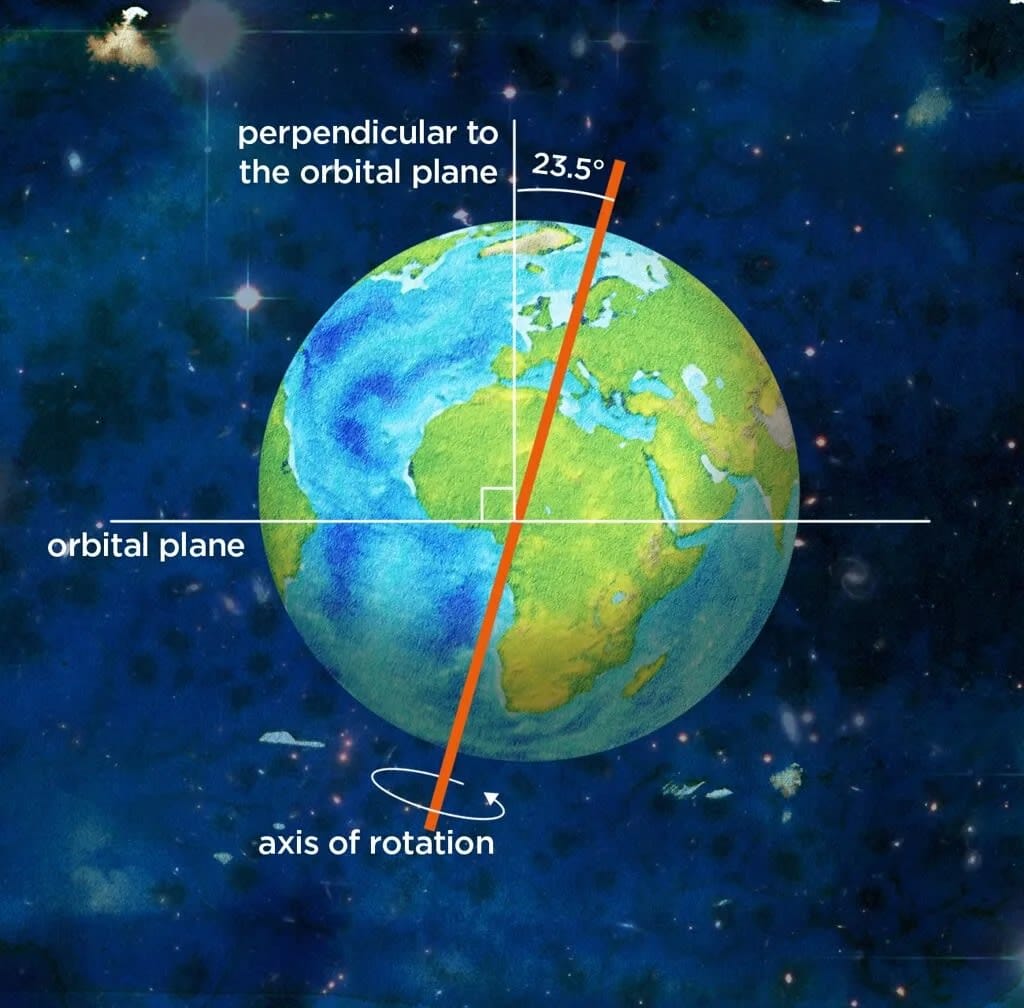
What this means is that the Earth’s axis, and consequently its equatorial plane, must be tilted at an angle of 23.44° to the plane of the Earth’s yearly orbit along the ecliptic. If there were no tilt, the Earth would revolve around the sun with its north pole pointing upwards, and the ecliptic and equator would be in the same plane. The sun would always set due west, and there’d be no seasons.
Another interesting deduction made by earlier astronomers is that these changing directions depend on the observer’s latitude. As the intriguing Elizabethan mathematician Thomas Harriot showed, there’s a formula giving the angle by which the direction deviates from due west at any given time of year at any particular location on Earth.
The formula uses the sun’s “declination”, the angle it makes with the celestial equator. It’s a different measurement from the solar “altitudes” that Ptolemy used in his calculation, which are measured with respect to the horizon. At the equinoxes, the sun appears to be “on” the equator, so its declination – its angle above the equator – is zero. The maximum declinations, which occur at the solstices, are ±23.44° (that is, 23.44°N and 23.44°S with respect to the equator).
Harriot knew all about how to take these different measurements, and how they related to the geometry of the celestial sphere – in the 1580s and 1590s, he was Sir Walter Raleigh’s navigational advisor, when Raleigh was sending fleets of sailing ships to America. And, like his famous contemporary Galileo Galilei, Harriot was also a Copernican.
In the 1590s, Harriot took his own careful measurements to update Ptolemy’s. He also wrote down the formula for the sunset directions: the sine of the deviation of the direction from due west = the sine of the sun’s declination at noon on the given day/the cosine of the observer’s latitude.
So, at the equinoxes, when the declination is zero and therefore so is its sine, the deviation of the direction of sunset is also zero, and the sun sets due west as expected.
For an observer at the equator, the latitude is zero, and cos 0 =1. So the deviation from due west is just the declination of the sun on that day. For instance, the maximum deviation, at the solstices, is 23.44°.
For all other latitudes, the cosine of the latitude is less than one, and since it's on the denominator of the equation, the maximum change in sunset direction is greater than 23.44°. For Melbourne, it's 30.3° away from due west, towards the south in summer and towards the north in winter.
A couple of months after the winter solstice, in the weeks around the September equinox, it’s wonderful to watch the setting sun making its way back towards the west, hovering there at the equinox, and then inching its way towards the south as the days get longer and spring finally arrives. And it’s fascinating that so much astronomical information lies hidden in such seemingly simple natural phenomena.





